 B .
B .  C .
C .  D .
D . 
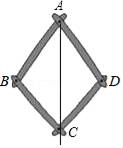

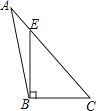 B .
B . 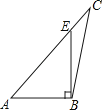 C .
C . 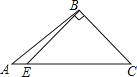 D .
D . 

分式 (
)的最大值是多少?
解: ,
因为x≥0,所以x+2的最小值是2,所以 的最大值是
,所以
的最大值是4,即
(x≥0)的最大值是4.
根据上述方法,试求分式 的最大值是.
小铭和小雨在学习过程中有如下一段对话:
小铭:“我知道一般当m≠n时,m2+n≠m+n2 . 可是我见到有这样一个神奇的等式: =
+(
)2(其中a,b为任意实数,且b≠0).你相信它成立吗?”
小雨:“我可以先给a,b取几组特殊值验证一下看看.”
完成下列任务:
①当a=,b=时,等式(填写“成立”或“不成立”);
②当a=,b=时,等式(填写“成立”或“不成立”).

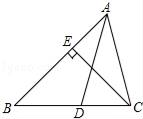
小明通过观察分析,形成了如下解题思路:如图2,延长AC到E,使CE=CD,连接DE.进而得到△ABD≌△AED,便可得到∠ACB与∠B的数量关系.请结合小明的思路,写出两个角的数量关系,并证明结论.

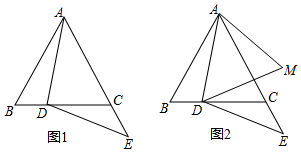
小明通过观察,实验提出猜想:在点D运动的过程中,始终有DA=AM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的两种想法:
想法1:要证明DA=AM,只需证△ADM是等边三角形;
想法2:连接CM,只需证明△ABD≌△ACM即可.
请你参考上面的想法,帮助小明证明DA=AM(选一种方法即可)