选择题(每题3分,共24分)
试题详情
我国明代数学读本《算法统宗》一书有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托。如果1托为5尺,那么索长和竿子长分别为多少尺?设索长为x尺,竿子长为y尺,可列方程组为( )
- A、
- B、
- C、
- D、
试题详情
如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A'B'C,点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为( )

- A、 α
- B、 α-45°
- C、 45°-α
- D、 90°-α
填空题(每题3分,共18分)
试题详情  =.
=.
试题详情
不等式2x+4≤0的解集为 .
试题详情  是关于x和y的二元一次方程ax+y=1的解,则a的值为 .
是关于x和y的二元一次方程ax+y=1的解,则a的值为 .
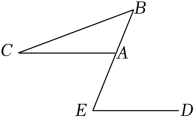
试题详情
如图,在灌溉时,要把河中的水引到农田  处,并要求所挖的渠道最短,小明画线段
处,并要求所挖的渠道最短,小明画线段  ,他的根据是.
,他的根据是.
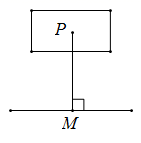
试题详情
如图所示的图案,至少要绕图案中心点旋转度后,才能与原来的图形重合.

试题详情
如图,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为.

解答题(78分)
试题详情
计算: .
.
试题详情
解方程组:
试题详情
解不等式: , 并把解集在数轴上表示出来.
, 并把解集在数轴上表示出来.
试题详情
被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342km,隧道累计长度的2倍比桥梁累计长度多36km.求隧道累计长度与桥梁累计长度.
试题详情
利用平方根的意义求方程(x-1)2=4中x的值.
试题详情
如图,在△ABC中,∠AED=80°,BD是∠ABC的平分线,DE∥BC,求∠EDB的度数.
试题详情
图①、图②、图③均是 的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中按下列要求作图,并保留必要的画图痕迹.
的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中按下列要求作图,并保留必要的画图痕迹.

试题详情
对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°.

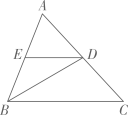
试题详情
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
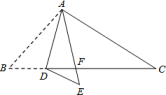
试题详情
我们在数学学习中,经常利用“转化”的思想方法解决问题,比如,我们通过“消元的方法将二元一次方程组转化为一元一次方程,从而求解.下面我们就利用“转化”的思想方法尝试解决新的问题.
先阅读下面的例题,再按要求完成下列问题.
例:解不等式(x-2)(x+1)>0.
解:由有理数的乘法法则“两数相乘,同号得正”,得①或②
解不等式组①,得x>2.
解不等式组②,得x<-1.
所以不等式(x-2)(x+1)>0的解集为x>2或x<-1.
根据例题方法解决下面问题:
试题详情
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a-2|+(b-3)2+ =0.
=0.